
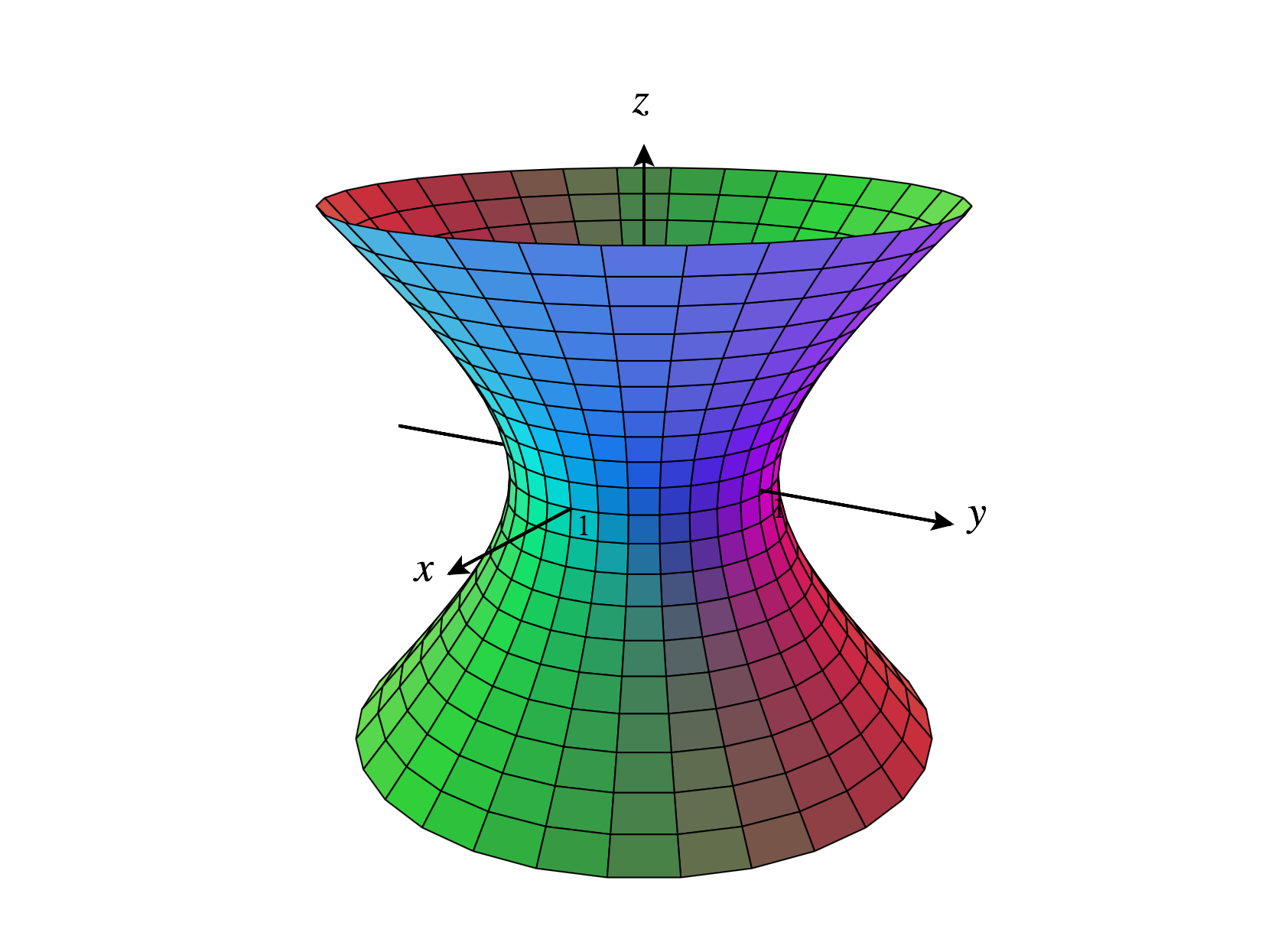
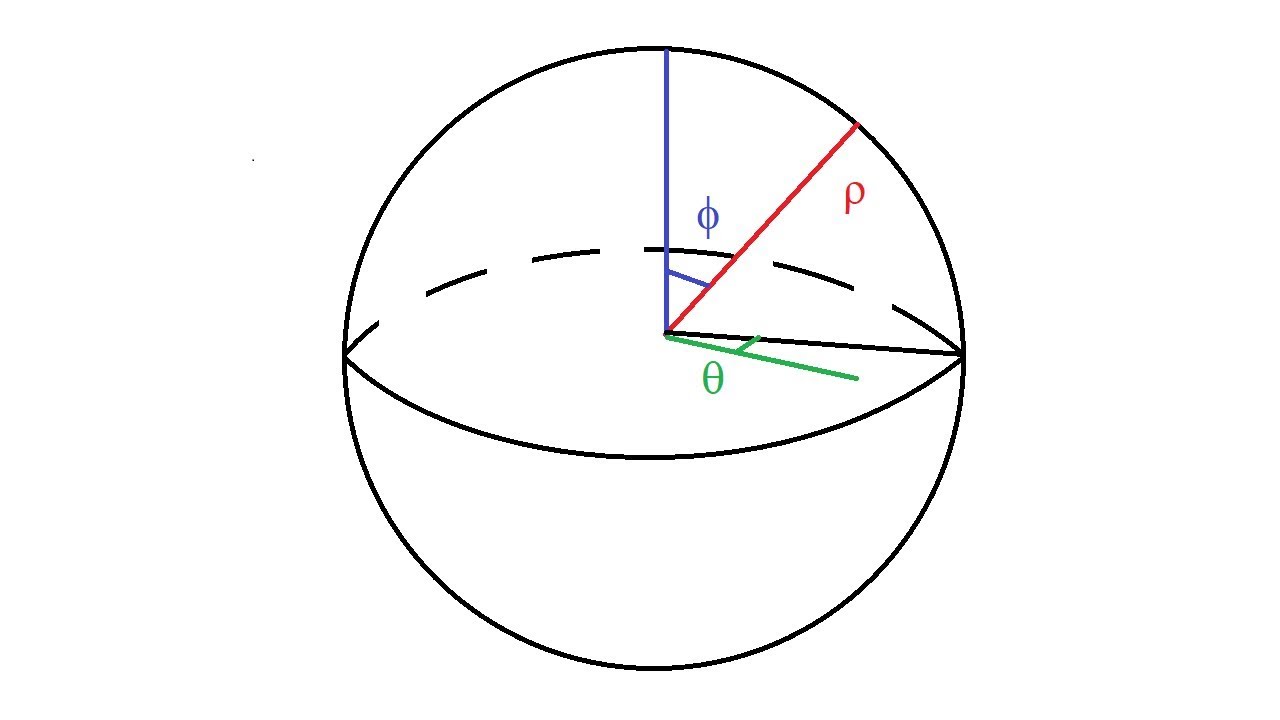
Dividing the coordinates of \(v_p\) by this length has the effect of normalizing \(v_p\). The relation between Cartesian and spherical coordinates is defined by. In two dimensions, the rectangular and the polar coordinate systems. The lecture on coordinate systems consists of 3 parts, each with their own video. The value \(\sin(\theta)\) represents the length of the vector \(v_p\) which is the vector v projected on the xy plane (Figure 9a). called cylindrical coordinates and spherical coordinates, that are sometimes better. Right: the x and y coordinates of the vector \(v_p\), once normalized, can be used to calculate phi (using atan2(y, x)). Left: the length of the vector \(v_p\) can be calculated using \(\sin(\theta)\). For values of \(\theta\) close to 0 or \(\pi\), \(v_p\) is very small (example on the left in Figure 8), and for values close to \(\pi/2\), \(v_p\) is longer (it lies on the unit circle when \(\theta=\pi/2\)). You can also notice that the length of the vector \(v\) projected in the xy plane (\(v_p\)) is directly related to the angle \(\theta\) (Figure 9). However, using atan2 to calculate \(\phi\) only works for the unit length vector. Technically speaking, the shadow of this vector corresponds to projecting the vector \(v\) on the xy plane. As you can see in Figure 8, even though the vector \(v\) is of unit length in world space, its shadow on the xy plane creates a vector that doesn't lie on the unit circle (unless \(\theta = \pi/2)\). This projected vector \((v_p)\) is shorter than a unit length vector, but to normalize it, we can divide it xy coordinates by \(\sin(\theta)\), which we then can use to calculate \(\sin(\phi)\) and \(cos(\phi)\).Ĭomputing \(\cos(\phi)\) and \(\sin(\phi)\) is also slightly more complicated. Still, we will need to convert them internally to radians to use them in the C++ trigonometric functions: \(\theta_įigure 8: the shadow of the yellow vector \((v)\) corresponds to the projection of \((v)\) on the xy plane. It will be easier to determine the angles in degrees. Note that the angle \(\theta\) is defined in radians. Similarly, the sine of this angle gives the y-coordinate of the point P. This angle is usually called \(\theta\) (the greek letter theta). When we draw a point P on this unit circle, the x-coordinate of the point can be calculated using the cosine of the angle subtended by the x-axis and a line that goes from the origin of the coordinate system to P. Spherical coordinates have the form (,, ). This can be used to represent points on the surface of a sphere. Usually, these functions are defined in regards to the unit circle (a circle of radius 1). Spherical coordinates allow points to be specified using one linear distances and two angles. Let's start to review the sine and cosine functions and how angles can be calculated from 2D coordinates. Rendering computer-generated images is almost entirely a geometric problem, so understanding and using trigonometry for creating such images (and the Pythagorean theorem) would be very hard. Trigonometric Functions Figure 1: the sine and cosine function can be used to find the coodinate of P which lies on the unit circle. This chapter is also an excellent opportunity to review trigonometric functions. We could certainly render images without using them, but you will see that using them simplifies many problems, especially regarding shading. Spherical Coordinates and Trigonometric Functions Reading time: 16 mins.īesides points, vectors, normals, and matrices, the last helpful technique from linear algebra we will need to render images is expressing vectors in terms of spherical coordinates. Creating an Orientation Matrix or Local Coordinate System.Spherical Coordinates and Trigonometric Functions.
For example, for an air parcel at the equator, the meridional unit vector, j →, is parallel to the Earth’s rotation axis, whereas for an air parcel near one of the poles, j → is nearly perpendicular to the Earth’s rotation axis. Note that the unit vectors in spherical coordinates change with position.


 0 kommentar(er)
0 kommentar(er)
